Formelsammlung

Ausfallsicherheit und Verfügbarkeit

$$Verf\ddot{u}gbarkeit=\frac{Betriebszeiten}{Betriebszeiten+Ausfallzeiten}=\frac{MTBF}{MTBF+MTTR}$$ $$Verf\ddot{u}gbarkeit=\frac{MengederObjekt-Mengedernichtverf\ddot{u}gbarenObjekte}{MengederObjekte}$$

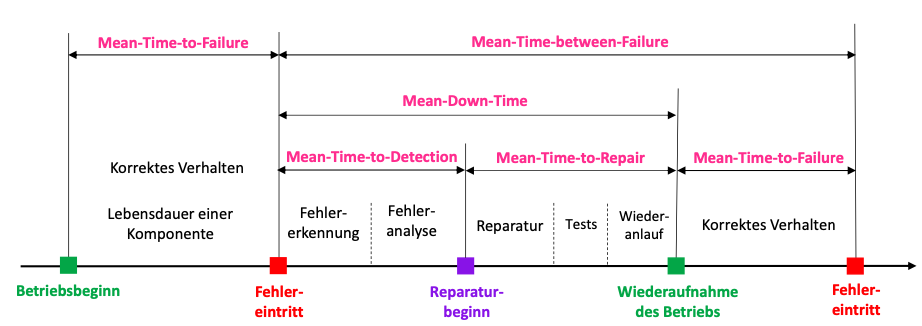
Systemverfügbarkeit

• Serienschaltung $V_{\text{Serie}}={\prod }_{i=1}^n{V}_i=V_{K_1}\cdot V_{K_2}\cdot \cdots \cdot V_{K_n}$

• Parallelschaltung $V_{\text{Parallel}}=1-{\prod }_{i=1}^n(1-V_i)=1-(1-V_{K_1})\cdot (1-V_{K_2})\cdot \cdots \cdot (1-V_{K_n})$

Beispiele

• Beispiel 1

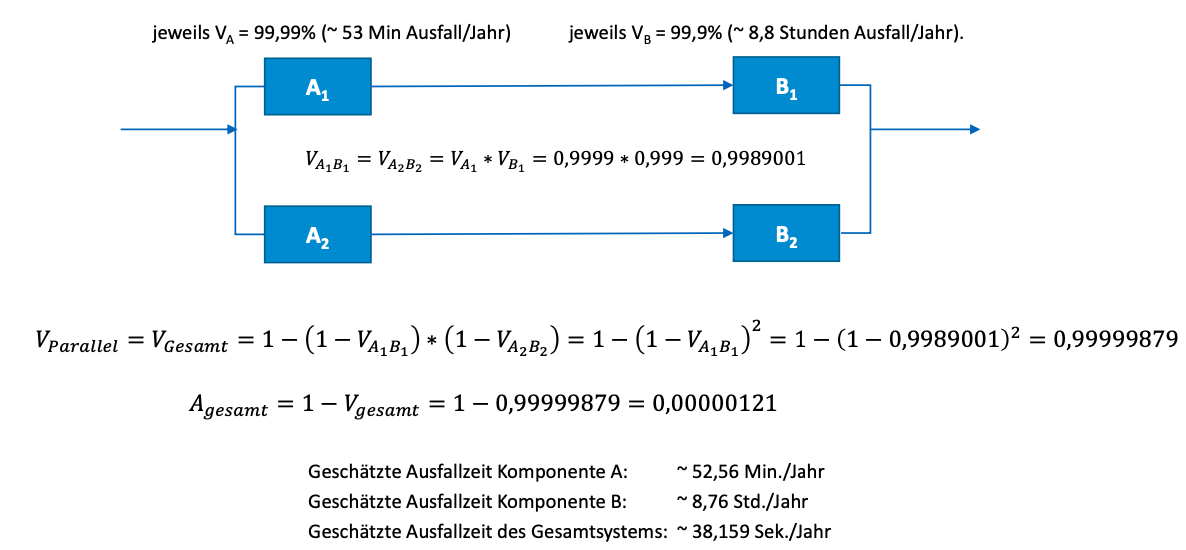
• Beispiel 2

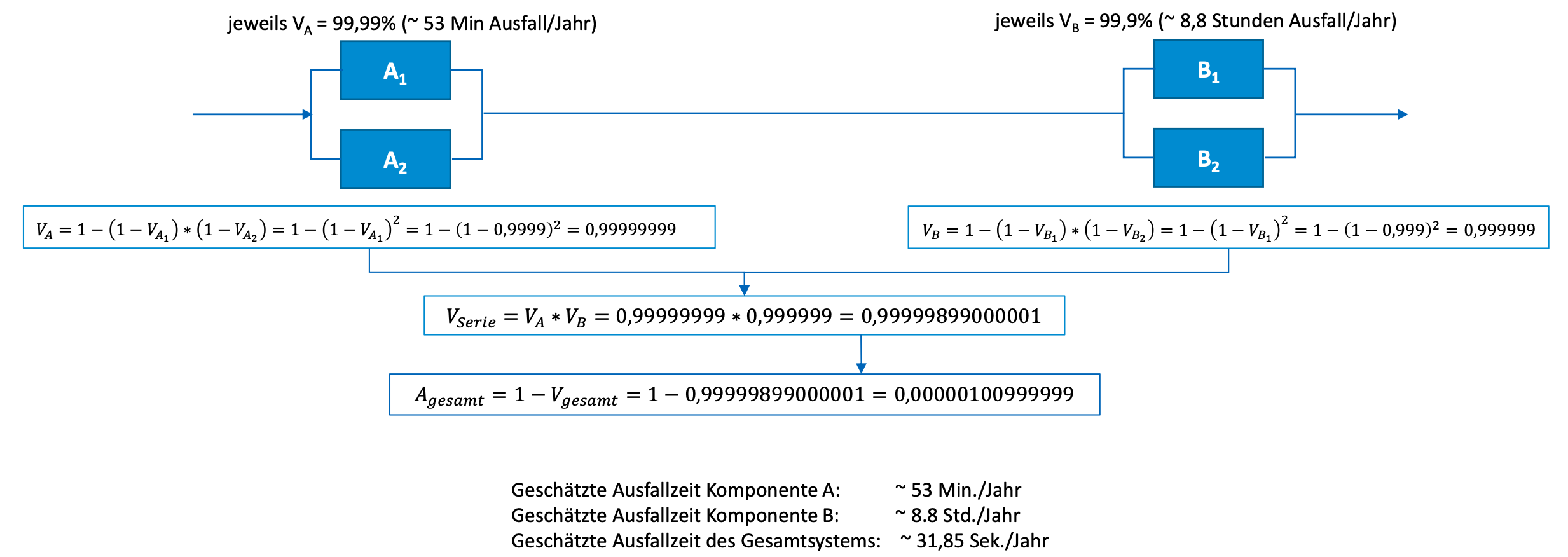
Klassifizierung der Verfügbarkeiten

Verfügbarkeitsklasse	Bezeichnung	Verfügbarkeit	Downtime
2	Stabil	99,0%	3,7 Tage/Jahr
3	Verfügbar	99,9%	8,8 Stunden/Jahr
4	Hochverfügbar	99,99%	52,2 Minuten/Jahr
5	Fehlerunempfindlich	99,999%	5,3 Minuten/Jahr
6	Fehlertolerant	99,9999%	32 Sekunden/Jahr
7	Fehlerresistent	99,999999%	3 Sekunden/Jahr

Die in TIA definierte Verfügbarkeitsstufen

Tier	Systementwurf	Verfügbarkeit / jährl. Ausfallzeit
1	- Anfällig für Unterbrechungen durch geplante und ungeplante Aktivitäten. - Ein Pfad für Strom- und Kühlungsverteilung, keine redundanten Komponenten. - Kann mit Doppelboden, USV oder Generator ausgestattet sein. - Implementierung dauert 3 Monate. - Wartungsarbeiten erfordern vollständige Abschaltung.	99,671% / 28,8 Stunden
2	- Weniger anfällig für Unterbrechungen durch geplante und ungeplante Aktivitäten. - Ein Pfad für Strom- und Kühlungsverteilung, inkl. redundanter Komponenten. - Beinhaltet Doppelboden, USV und Generator. - Implementierung dauert 3 bis 6 Monate. - Wartung des Stromnetzes erfordert Abschaltung der Verarbeitung.	99,741% / 22,0 Stunden
3	- Ermöglicht geplante Aktivitäten ohne Betriebsunterbrechung, aber ungeplante Ereignisse können Unterbrechungen verursachen. - Mehrere Verteilungspfade für Strom und Kühlung, jedoch nur ein aktiver Pfad. - Beinhaltet redundante Komponenten. - Implementierung dauert 15 bis 20 Monate. - Beinhaltet Doppelboden und ausreichende Kapazität für Lcdotübernahme während Wartung.	99,982% / 1,6 Stunden
4	- Geplante Aktivitäten stören die kritische Lcdot nicht. - Rechenzentrum kann mindestens ein ungeplantes Ereignis bewältigen. - Mehrere aktive Strom- und Kühlungsverteilungspfade, inkl. redundanter Komponenten. - Implementierung dauert 15 bis 20 Monate.	99,995% / 0,4 Stunden

Softwarequalität

Fehlerdichte (pro 1.000 LOC)	Klassifizierung
< 0,5	stabil
0,5 … 3	reif
3 … 6	labil
6 … 10	fehleranfällig
> 10	unbrauchbar

Authentifikationen durch Wissen

Entropy von Passwort

$$Entropie=lo{g}_2(Zeichensat{z}^{(Passwortl\ddot{a}nge)})=Passwortl\ddot{a}nge\cdot lo{g}_2(Zeichensatz)$$

Umstellen nach Passwortlänge:

$$\text{Passwortla¨nge}=\frac{\text{Entropie}}{{\log }_2(\text{Zeichensatzgro¨ße})}$$

Umstellen nach Zeichensatzgröße:

$$\text{Zeichensatzgro¨ße}=2^{\frac{\text{Entropie}}{\text{Passwortla¨nge}}}$$

Beispiel

Gegeben sind: - $Passwortl\ddot{a}nge=4$ - $Zeichensatz=83$

$$Entropie=4\cdot lo{g}_2(83)=4\cdot \frac{In(83)}{In(2)}=25\text{ Bits}$$

• Nicht aufrunden!

---

Entropy of Passphrases

$$Entropie=lo{g}_2(W\ddot{o}rterbuchumfan{g}^{(AnzahlW\ddot{o}rter)})=AnzahlW\ddot{o}rter\cdot lo{g}_2(W\ddot{o}rterbuchumfang)$$

Umstellen nach Anzahl Wörter:

$$\text{Anzahl Wo¨rter}=\frac{\text{Entropie}}{{\log }_2(\text{Wo¨rterbuchumfang})}$$

Umstellen nach Wörterbuchumfang:

$$\text{Wo¨rterbuchumfang}=2^{\frac{\text{Entropie}}{\text{Anzahl Wo¨rter}}}$$

Beispiel

Gegeben sind: - $W\ddot{o}rterbuchumfang=4$ - $AnzahlW\ddot{o}rter=145.000$

$$Entropie=4\cdot lo{g}_2(145.000)=4\cdot \frac{In(145.000)}{In(2)}=68\text{ Bits}$$

• Nicht aufrunden!

Biometrische Systeme

Kennzahlen zur Leistungsfähigkeit des Systems

False Acceptance Rate (FAR)

Die FAR ist die Wahrscheinlichkeit, dass ein biometrisches System nicht-affine Merkmal akzeptiert.

$$FAR=\frac{\text{Anzahl der positiven Vergleiche nicht affiner Merkmale}}{\text{Gesamtanzahl der Vergleiche nicht affiner Merkmale}}$$

False Rejection Rate (FRR)

Die FAR ist die Wahrscheinlichkeit, dass ein biometrisches System affine Merkmal zurückweist.

$$FRR=\frac{\text{Anzahl der negativen Vergleiche nicht affiner Merkmale}}{\text{Gesamtanzahl der Vergleiche nicht affiner Merkmale}}$$

Hamming Code

Empfangenes Codewort:

Bit-Nr.	1	2	3	4	5	6	7
Beispiel	1	0	1	0	1	1	0

1. Bestimme die Prüfbitpositionen und die geprüften Nutzbits

Zur Bestimmung, welche Bits als Prüfbits fungieren, wandeln wir die Stellennummern in Binärdarstellung um.

Bit-Nr.	Binär
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111

• Alle mit 1 endenden Binärdargestellten Wörter sind vom Prüfbit an der Position 2^0 geprüft.
• Alle Bitstrings mit 1 am vorletzten Bit werden vom Prüfbit an der Position 2^1 geprüft.
• usw.

2. Vergleich mit empfangenen Parity-Bits

XORisierung aller zusammengehöriger Bits

• $C_1=(Bi{t}_1+Bi{t}_3+Bi{t}_5+Bi{t}_7\mathrm{mod}2=1+1+1+0\mathrm{mod}2=1$
• $C_2=(Bi{t}_2+Bi{t}_3+Bi{t}_6+Bi{t}_7\mathrm{mod}2=0+1+1+0\mathrm{mod}2=0$
• $C_3=(Bi{t}_4+Bi{t}_5+Bi{t}_6+Bi{t}_7\mathrm{mod}2=0+1+1+0\mathrm{mod}2=0$

3. Diagnose

Stelle die $C$-Bits in absteigender Reihenfolge dar und wandle in Dezimal um, das Ergebnis ist das gekippte Bit. im Beispiel ist Syndrom = 001 → $Bi{t}_1$ ist falsch!

Verschlüsselung

Indisches Schema

Prüfe für $n=60$ und $a=47$, dass $ggT(n,a)=ggT(60,47)=1$ ist und bestimme $a^{-1}$

• Es gilt: $n=q\cdot a+r=1\cdot 47+13=60$

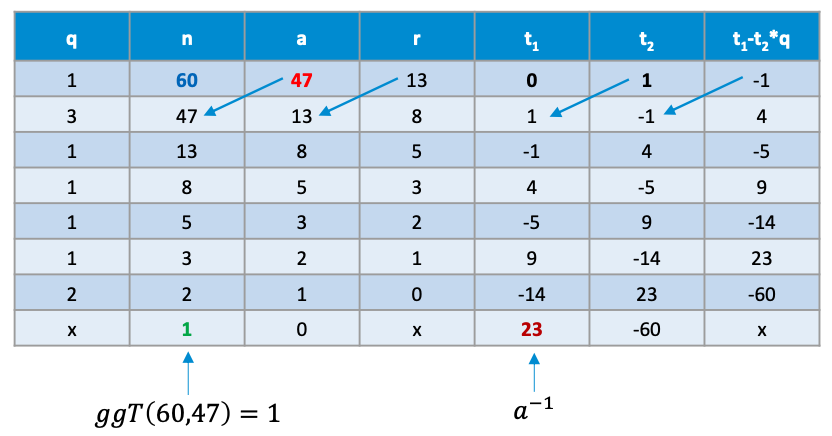
Substitionstechniken

Ein monoalphabetischer Substitution-Verschlüsselungsalgorithmus

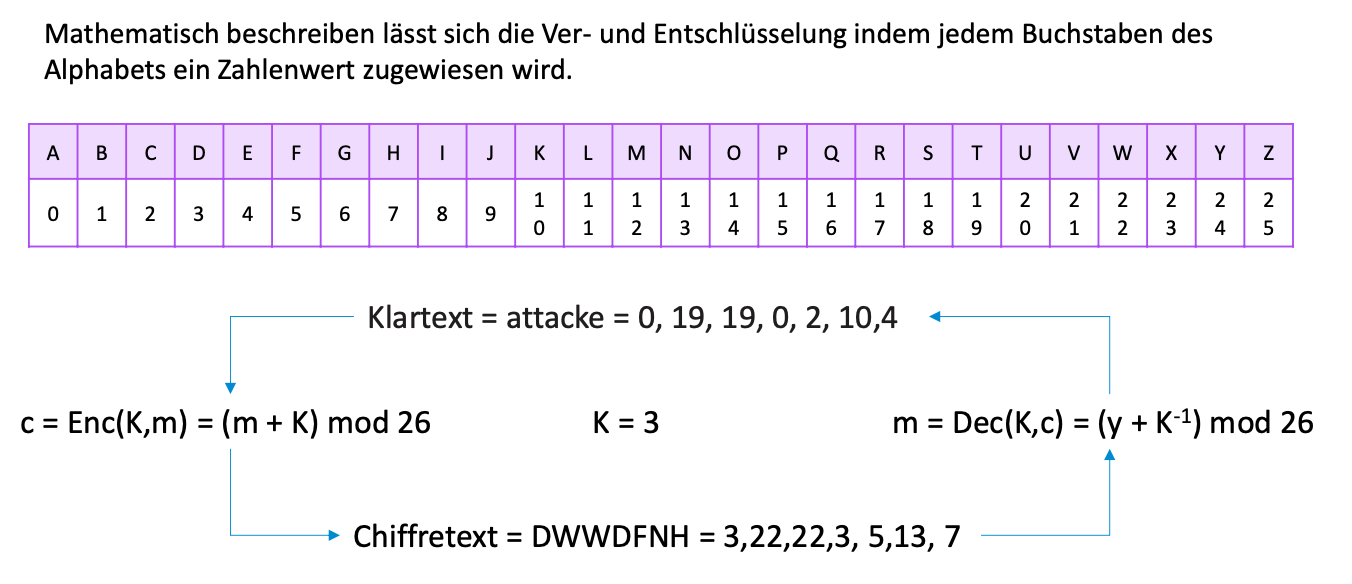
Vigenère Ciffre, eine polyalphabetische Chiffre

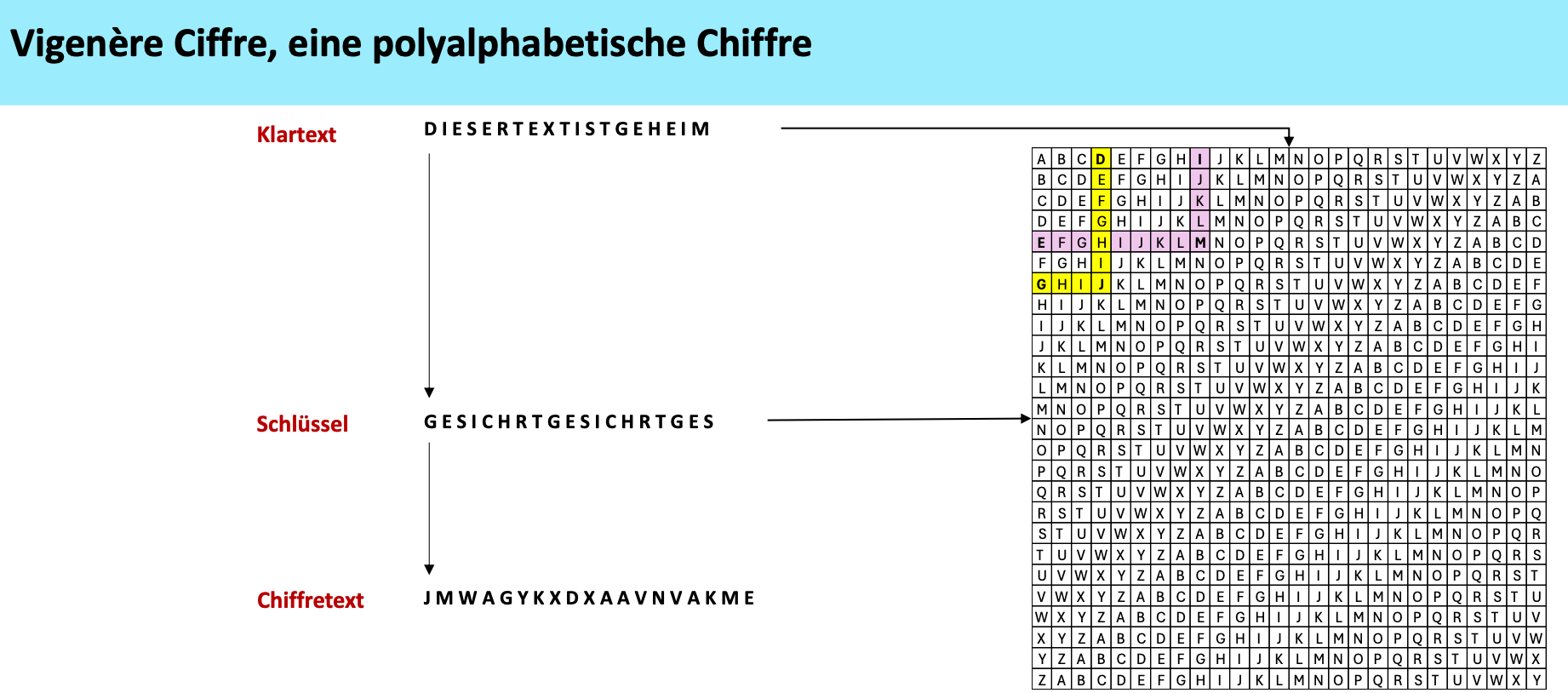
Transpositionstechniken

Rail-Fence-Technik

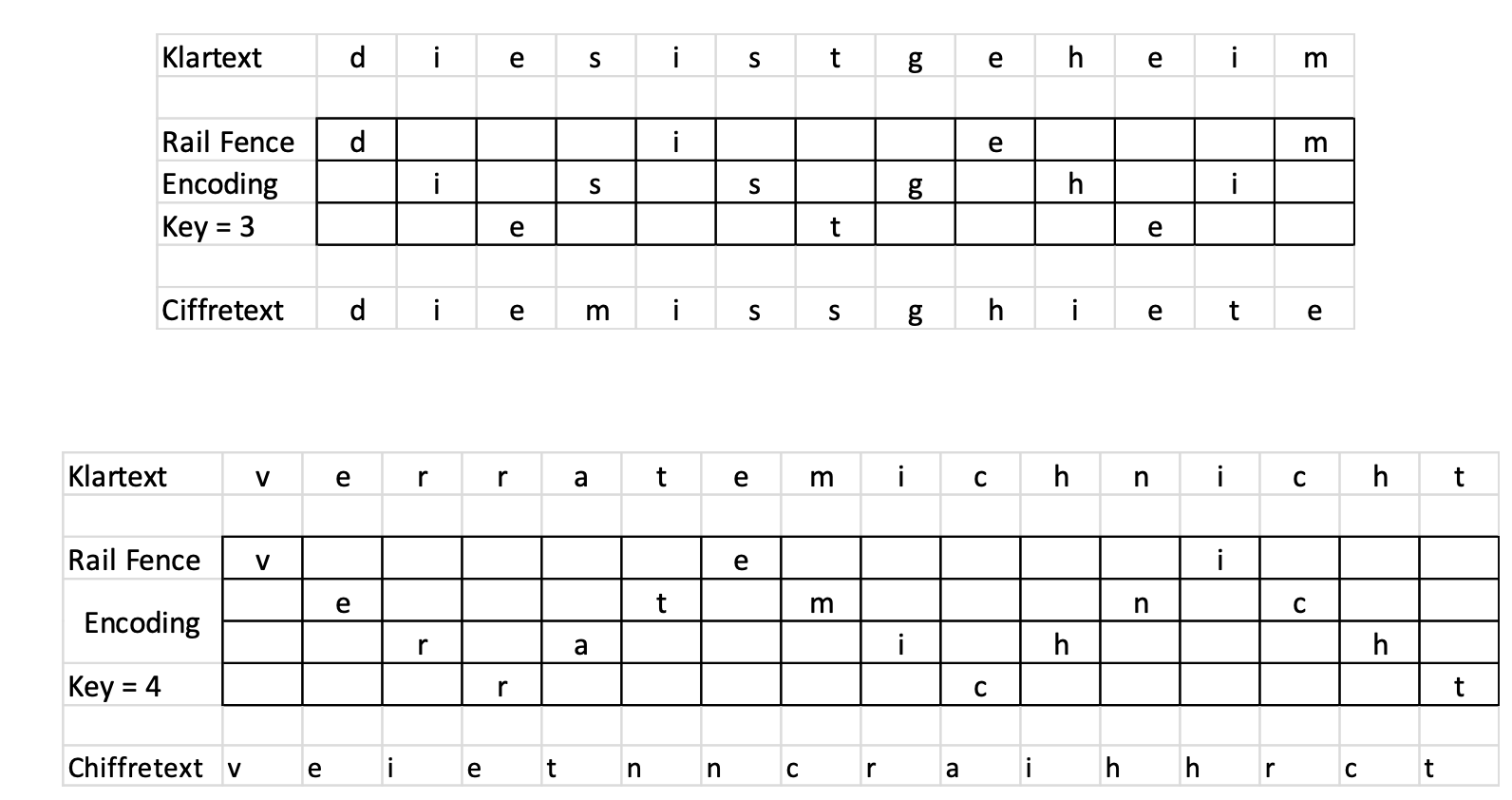
Doppelte Transposition

Diffie-Hellmann

Definitionen

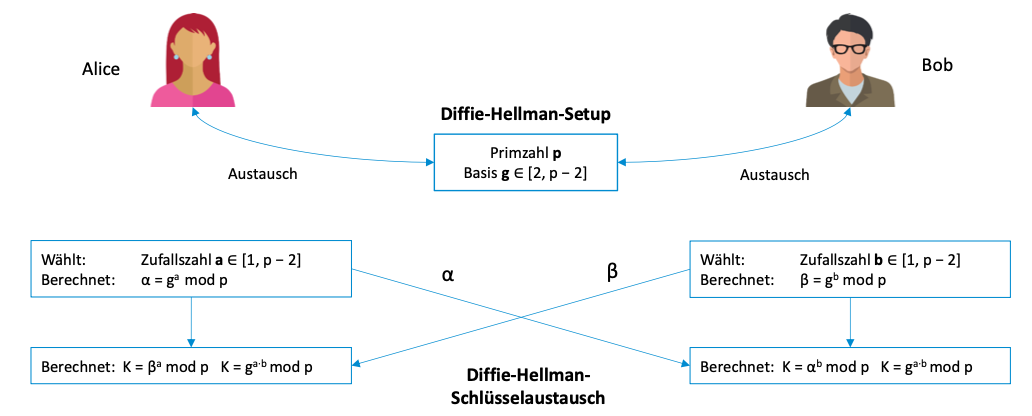
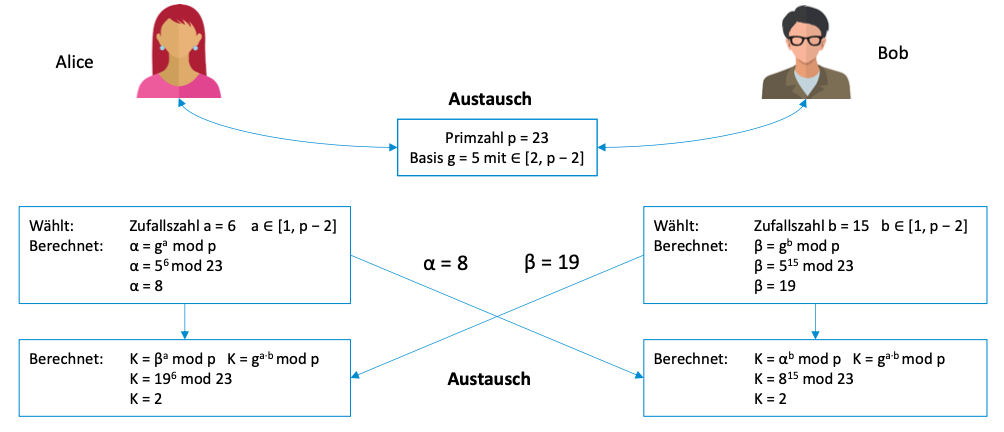
Beispiel

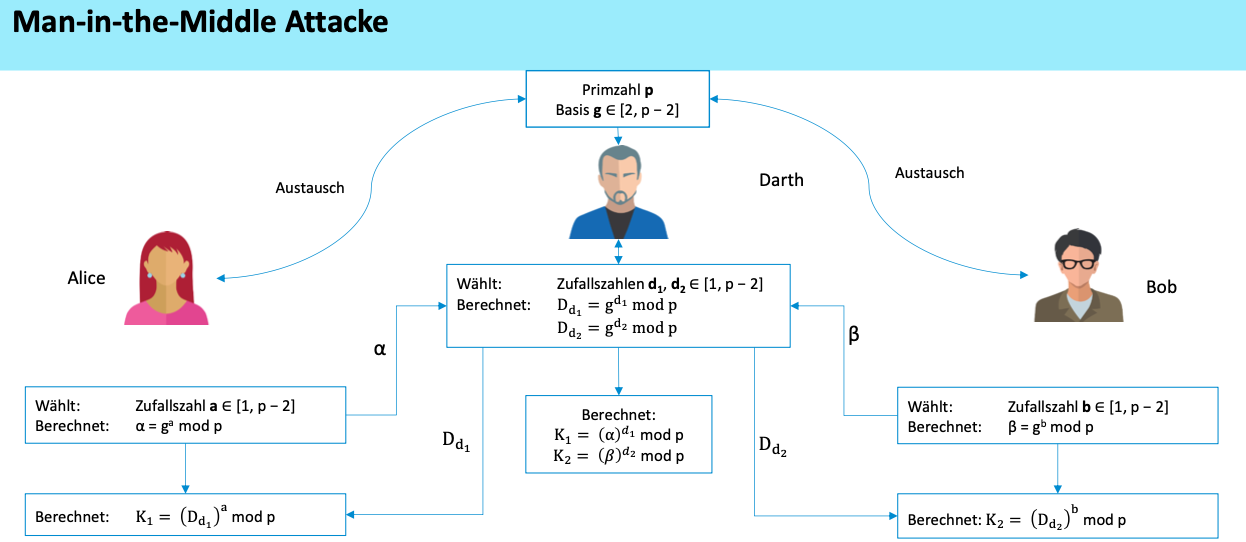
Man-in-the-Middle Attacke

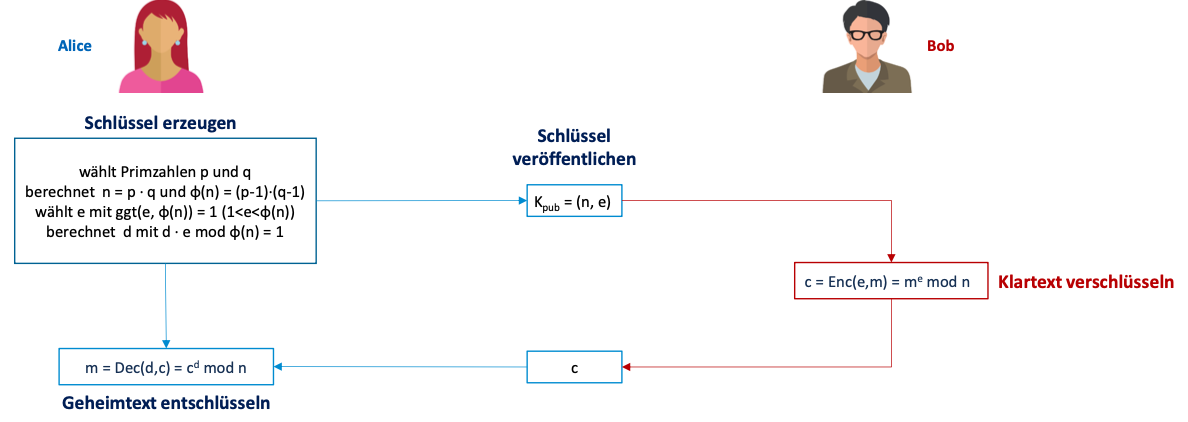
RSA-Algorithmus

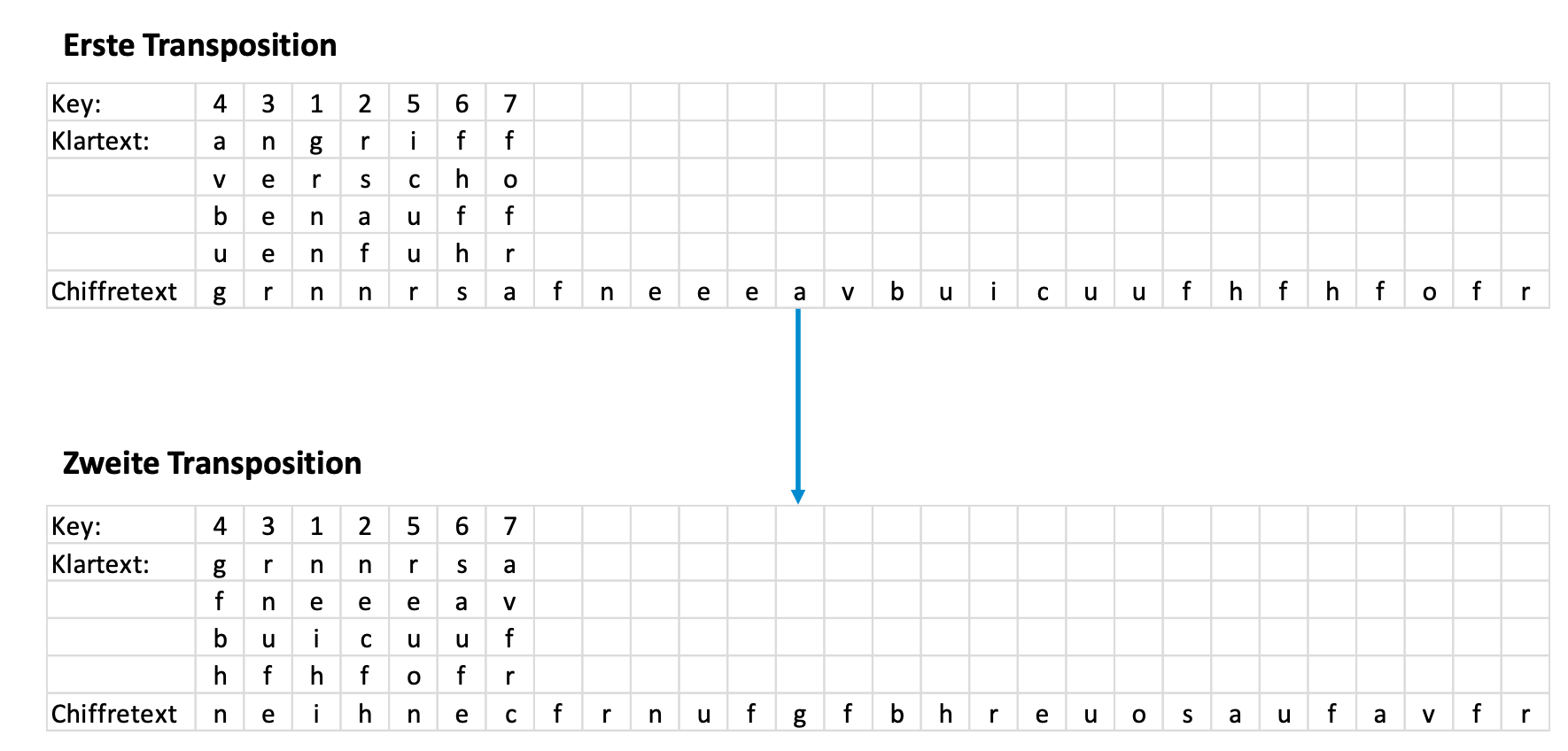
Ver- und Entschlüsselungen

Beispiel

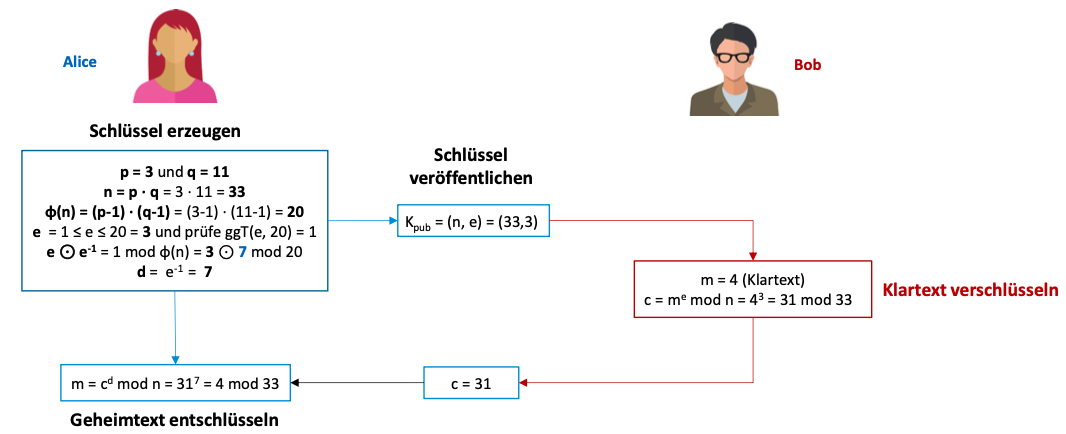
RSA-Signatur

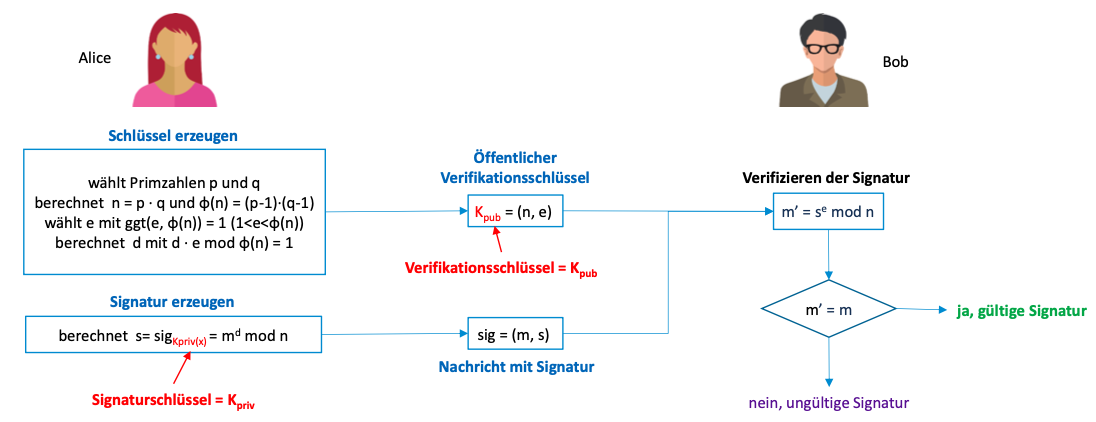
Beispiel

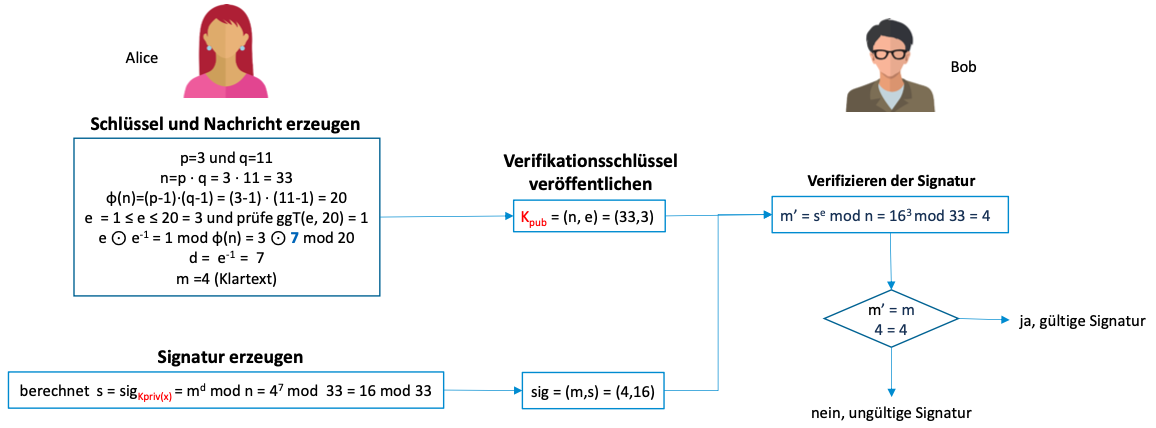
Homomorphe Verschlüsselung

Multiplikative und additive homomorphen Verschlüsselungssysteme

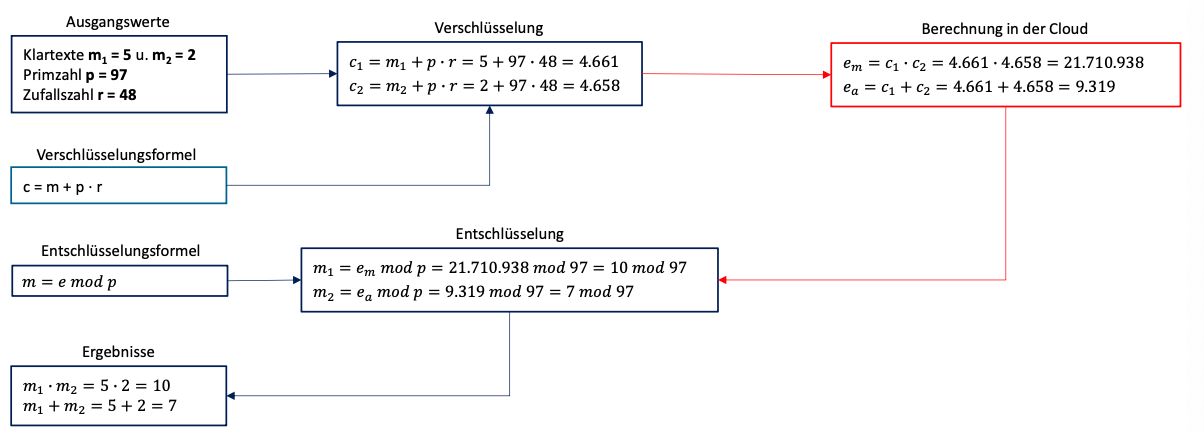
RSA ein Beispiel eines multiplikativen homomorphen Verschlüsselungssystems

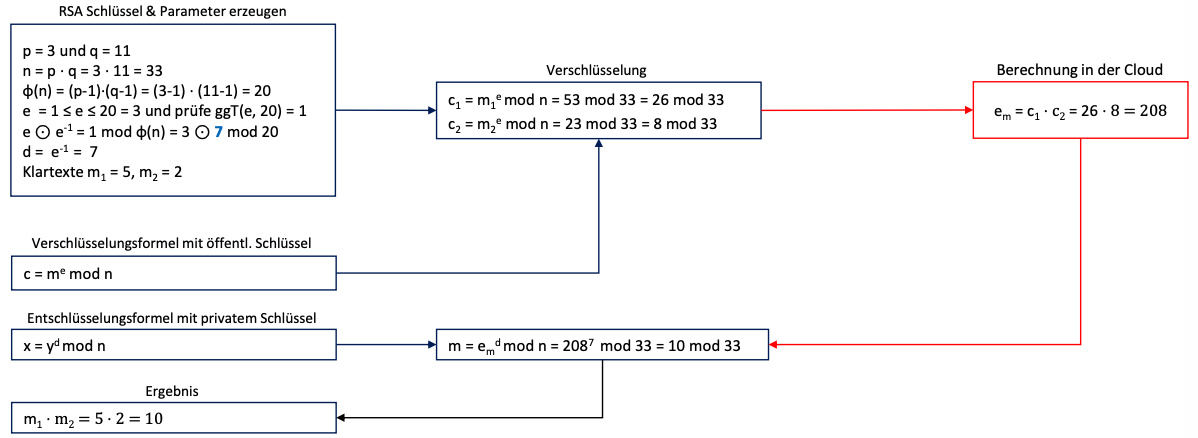
Zusammenfassungen

Diffie-Hellman

Alice und Bob möchten einen Schlüssel austauschen. Sie einigen sich öffentlich auf die Primzahl $p=19$ und eine Basis $g=5$ aus dem Galois-Körper $GF(19)$ (→ $n=19$). Alice wählt die Zufallszahl $a=2$ und Bob $b=10$.

beide Parteien berechnen $\alpha$ und $\beta$

• Alice: $\alpha =g^a\mathrm{mod}n=5^2\mathrm{mod}19=6$
• Bob: $\beta =g^b\mathrm{mod}n=5^{1}0\mathrm{mod}19=5$

Anschließend schickt jede Partei den errechneten Wert der jeweils anderen Partei.

Schlüssel berechnen

Jede Partei kann auf seiner Seite den Schlüssel durch den empfangenen Wert berechnen.

• Alice: $K={\beta }^a\mathrm{mod}n=5^2\mathrm{mod}19=6$
• Bob: $K={\alpha }^b\mathrm{mod}n=6^{1}0\mathrm{mod}19=6$

RSA-Algorithmus

Verschlüsselung

Alice möchte Bob eine verschlüsselte Nachricht schicken. Dazu berechnet Bob seinen public & private Key.

Public & Private Key berechnen

Wählen Sie im Laufe der Berechnung als public Key $e=17$ und prüfen Sie, ob $e$ ein valider Schlüssel ist. Berechnen Sie Bobs private Key auf Basis der Primzahlen $p=37$ und $q=17$.

1. Berechnung des Modulus $n$

   $n=p\cdot q=37\cdot 17=629$

2. Berechnung der Phi-Funktion $\varphi (n)$

   $\varphi (n)=(p-1)\cdot (q-1)=36\cdot 16=576$

3. Validierung des public Keys $e$

   Der öffentliche Schlüssel muss folgende Bedingungen erfüllen:

   1. $1<e<\varphi (n)$ → 17 erfüllt das im Beispiel
   2. $e$ und $\varphi (n)$ müssen teilerfremd sein ($ggT(e,\varphi (n))=1$) → $e=17$ ist eine Primzahl, es muss also nur gezeigt werden, dass $576\mathrm{mod}17\ne 0$ ist → $15\ne 0$ → public Key ist gültig!

4. Berechnung des private Keys $d$

   Der private Key $d$ ist das multiplikative Inverse von $e$ modulo $\varphi (n)$.

   $d\cdot e=1\mathrm{mod}\varphi (n)$

   Zur Berechnung kann man den erweiterten euklidischen Algorithmus nutzen:

   • (t1 und t2 werden mit 0 und 1 initialisiert)

   q	n	a	r	t1	t2	t1-t2 * q
   33	576	17	15	0	1	-33
   1	17	15	2	1	-33	34
   7	15	2	1	-33	34	-271
   2	2	1	0	34	-271	32

   Wenn r = 0 ist, ist der letzte Wert von a der ggt(n,a) und t2 das multiplikative Inverse $a^{-1}$. Im Beispiel gilt $d=-271+576=305$.

Verschlüsseln einer Nachricht $m$

Nutzen Sie den Public Key $e=17$ von Bob, um die Nachricht $m=65$ zu verschlüsseln.

• Cypher $c=m^e\mathrm{mod}n=65^{17}\mathrm{mod}629=337$

Entschlüsseln von $c$ als Prüfung

• Message $m=c^d\mathrm{mod}n=337^{305}\mathrm{mod}629=65$

Signatur

Bob möchte eine Nachricht signieren, damit Alice sicher sein kann, dass die Nachricht von ihm stammt.

Public & Private Key berechnen

Wählen Sie im Laufe der Berechnung als public Key $e=3$ und prüfen Sie, ob $e$ ein valider Schlüssel ist. Berechnen Sie Bobs private Key auf Basis der Primzahlen $p=3$ und $q=11$.

1. Berechnung des Modulus $n$

   $n=p\cdot q=3\cdot 11=33$

2. Berechnung der Phi-Funktion $\varphi (n)$

   $\varphi (n)=(p-1)\cdot (q-1)=2\cdot 10=20$

3. Validierung des public Keys $e$

   Der öffentliche Schlüssel muss folgende Bedingungen erfüllen:

   1. $1<e<\varphi (n)$ → 3 erfüllt das im Beispiel
   2. $e$ und $\varphi (n)$ müssen teilerfremd sein ($ggT(e,\varphi (n))=1$) → $e=3$ ist eine Primzahl, es muss also nur gezeigt werden, dass $20\mathrm{mod}3\ne 0$ ist → $2\ne 0$ → public Key ist gültig!

4. Berechnung des private Keys $d$

   Der private Key $d$ ist das multiplikative Inverse von $e$ modulo $\varphi (n)$.

   $d\cdot e=1\mathrm{mod}\varphi (n)$

   Zur Berechnung kann man den erweiterten euklidischen Algorithmus nutzen:

   • ggT(20, 3)
   • (t1 und t2 werden mit 0 und 1 initialisiert)

   q	n	a	r	t1	t2	t1-t2 * q
   6	20	3	2	0	1	-6
   1	3	2	1	1	-6	7
   2	2	1	0	-6	7	-26

   Wenn r = 0 ist, ist der letzte Wert von a der ggt(n,a) und t2 das multiplikative Inverse $a^{-1}$. Im Beispiel gilt $d=7$.

Signieren einer Nachricht $m$

Nutzen Sie den Private Key $d=7$ von Bob, um die Nachricht $m=4$ zu signieren.

• Signatur $s=m^d\mathrm{mod}n=4^7\mathrm{mod}33=16$

→ Nachricht mit Signatur $sig=(m,s)=(4,16)$

Verifizieren der Signatur

• Message $m^{\prime }=s^e\mathrm{mod}n=16^3\mathrm{mod}33=4$
• $m^{\prime }=m$ → Signatur ist gültig!
• Sonst: Signatur ist ungültig!
• Hier: $4=4$ → Signatur ist gültig!

Homomorphe Verschlüsselung

• Primzahl $p=131$
• Zufallszahl $r=46$

Verschlüsselung

Berechne $c_1$ und $c_2$ aus den Klartextwerten $m_1=13$ und $m_2=7$.

$c_1=m_1+p\cdot r=13+131\cdot 46=6039$ $c_2=m_2+p\cdot r=7+131\cdot 46=6033$

Multiplikation und Addition

Addiere und Multipliziere die Werte jeweils miteinander.

$ad{d}_{enc}=c_1+c_2=6039+6033=12072$ $mu{l}_{enc}=c_1\cdot c_2=6039\cdot 6033=36433287$

Entschlüsseln der Ergebnisse

Entschlüssle $ad{d}_{enc}$ und $mu{l}_{enc}$.

$add=ad{d}_{enc}\mathrm{mod}p=12072\mathrm{mod}131=20$ $mul=mu{l}_{enc}\mathrm{mod}p=36433287\mathrm{mod}131=91$

Überprüfung

$add=13+7=20$ $mul=13\cdot 7=91$