Neuronale Netze

Neuronale Netze sind von der Struktur des menschlichen Gehirns inspirierte Modelle, die aus miteinander verbundenen Neuronen bestehen. Sie sind besonders leistungsstark bei der Bewältigung komplexer Aufgaben und haben in den letzten Jahren durch Fortschritte in der Hardware und neue Entwicklungen in der Architektur an Bedeutung gewonnen.

Grundidee

• Inspiration durch das Gehirn: Neuronale Netze sind dem menschlichen Gehirn nachempfunden, das aus einem Netzwerk von Neuronen besteht.
• Komplexe Berechnungen: Durch die Vernetzung von Neuronen können komplexe Berechnungen durchgeführt werden.

Neuronen

• Grundbausteine: Neuronen sind die fundamentalen Einheiten neuronaler Netze.
• Funktion: Jedes Neuron repräsentiert eine einfache Funktion, die aus den Eingabedaten einen Ausgabewert berechnet.
• Gewichtete Summe: Im einfachsten Fall wird die gewichtete Summe der Eingabedaten berechnet. $$y=b_1\cdot \ast x_i+b_2\cdot x_2+\cdots +b_n\cdot x_n$$

  • dies führt zu zwei Problemen

    • Beim Vernetzen von Neuronen ist die Ausgabe eines Neurons die Eingabe des nächsten Neurons..
      • Immer weiter aufsummieren → wird es numerisch schwerig, große Netzwerke zu erstellen
    • Beim Klassifizieren mit neuronalen Netzen werden die ==diskrete Ergebnisse (0/1) benötigt
      • Schwer zu realisieren.

  • Um diese Probleme zu vermeiden, wird mit Aktivierungsfunktionen gearbeitetn.

• Aktivierungsfunktionen: Um die Ausgabewerte zu begrenzen und nichtlineare Beziehungen zu modellieren, werden Aktivierungsfunktionen verwendet, wie z. B. die Sigmoid-Funktion.

Aktivierungsfunktion

• bildet die gewichteten Summen der Eingänge auf feste Ausgabebereiche ab.
• Häufige Aktivierugnsfunktion ist die `Sigmoid-Funtkion $S_a:$ → $[0,1]$, die für einen Steigungsparameter $a$ definiert ist durch:

$$S_a(x):=\frac{1}{1+e^{-ax}}$$

Schöne Eigenschaft von Sigmoid-Funktion

Sie ist differenzierbar 🥹 und liefert einen Wert zwischen 0 und 1, was als Wahrscheinlichkeit betrachtet werden kann.

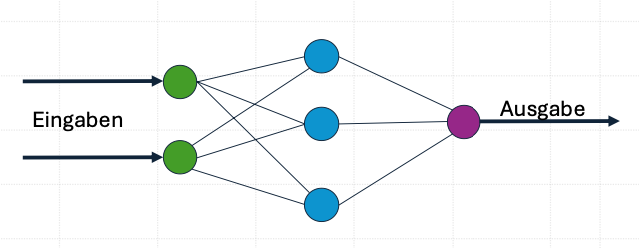
Vernetzung von Neuronen

• Verbindungen: Neuronen sind miteinander verbunden, sodass die Ausgabe eines Neurons als Eingabe für ein anderes Neuron dient.
• Schichten: Typischerweise werden Neuronen in Schichten angeordnet.
  • Eingabeschicht: Empfängt die Eingabedaten.
  • Verdeckte Schichten: Verarbeiten die Daten in mehreren Schritten.
  • Ausgabeschicht: Liefert die endgültige Ausgabe des Netzes.
• Feedforward-Netze: Netze ohne Rückkopplungen.
• Rekurrente neuronale Netze: Netze mit Rückkopplungen, die Informationen aus früheren Zeitschritten speichern können.

Training des neuronalen Netzes

Anpassung der Gewichte

Die Gewichte der Verbindungen zwischen den Neuronen werden während des Trainings angepasst, um die gewünschte Ausgabe zu erzielen.

Initialisierung mit Zufallswerten

Zu Beginn werden die Gewichte zufällig initialisiert.

Vergleich von Ist- und Soll-Ausgabe

Die Ausgabe des Netzes wird mit der erwarteten Ausgabe (Soll-Wert) aus den Trainingsdaten verglichen.

Gradientenabstiegsverfahren

Ein Optimierungsverfahren, das die Gewichte schrittweise anpasst, um die Abweichung zwischen Ist- und Soll-Ausgabe zu minimieren.

• Dabei werdne die Menge der Trainingsdaten in Batches (Epoche) aufgeteilt.
• Bei jedem Iterationsschritt wird für einen anderen Batch die Kostensumme bestimmt.
• Eine Epoche entsteht, wenn die Gesamte Trainingsdatenmenge einmal durchgelaufen wurde.

Stochastic Gradient Descent

Eine Variante des Gradientenabstiegsverfahrens, bei der nur eine Teilmenge der Trainingsdaten pro Iteration verwendet wird, um die Berechnungen zu beschleunigen.

Backpropagation

Ein Algorithmus, der die Anpassung der Gewichte effizient berechnet, indem er die Fehlersignale von der Ausgabeschicht zurück zur Eingabeschicht propagiert.

die Backpropagation verringert den Optimierungsaufwand drastisch. Ohne es währe das Training komplexer Nezte nicht möglich.

Neuronale Netze in Python

Daten skalieren

Das neuronale Netz, das wir verwenden (MLP = Multi-Layer Perceptron) arbeitet mit skalierten Daten besser.

from sklearn.preprocessing import StandardScaler
 
scaler = StandardScaler()
scaler.fit(X_train)
 
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
 

Neuronales Netz trainieren

scikit-learn bietet als Klassifikationsverfahren das Multi-Layer Perceptron an. Das sind die einfachen mehrschichtigen Netzwerke.

from sklearn.neural_network import MLPClassifier
 
#in hidden_layer_sizes gibt es drei Schichten, die erste 30, die zweite 20 und die dritte 10
model = MLPClassifier(solver='lbfgs', max_iter=20000, alpha = 1, 
                      hidden_layer_sizes=(30,20,10) , random_state = 0)
 
model.fit(X_train, y_train)
print(model.score(X_test, y_test))

• max_iter ist die Anzahl Iterationsschritte nach denen der Gradientenabstieg abbricht
• hidden_layer_sizes Anzahl der Neuronen in den einzelnen versteckten Schichten.
• alpha ein Parameter für einen Regulatrisierungsterm, der eine Überanpassung an die Trainingsdaten bestraft.

Je größer alpha, desto eher passt sich das neuronale Netz dem allgemeinen Trend an